Views in Seashell

This document presents Views which are Seashell’s zero-cost abstraction for structured iteration. The Seashell type system provides a safe access guarantee, i.e., a program that typechecks never tries to access the same memory bank in the same cycle. To provide this guarantee, the type system needs the programmer to expose the iteration pattern they are using on a logical array in the program. Views provide a mechanism to expose the iteration pattern to the type system without having to pay the cost of creating a new memory bank. Views are a zero-cost abstraction because they only exist in Seashell and are compiled into simple array accesses.

Note on syntax

This proposal uses a verbose syntax for view creation. The surface language instead uses the syntax:

v_a = view a[off:w:s]

Creating views

A view, as it’s name suggests, is a logical view over a pre-existing array. To create a view we use the following syntax:

int[8 bank(2)] a;
v_a = view[w=2, off=0] a;

This creates a view v_a on array a that has width (w) of 2. The off represents the starting point of the view. A view expression also consumes array a from the current context which means a can no longer be accessed in the current scope. The variable v_a created from this view expression simply acts as an array. For example, we can write:

for (i = 0..2) {
    v_a[i] := 10
}

However, the view in this example isn’t very interesting since it remains static. In order to specify an iteration strategy using a view, we can use a dynamic off value:

int [8 bank(2)] a;
for (i = 0..3) {
    v_a = view[w=2, off=i];
}

which creates the following iteration pattern:

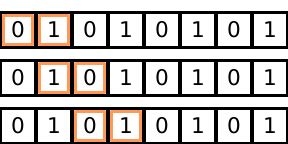
And again, since v_a just acts as a simple array, we can do the following:

for (i = 0..3) {
    v_a = view[w=2, off=i];
    for (j = 0..2) {
        v_a[j] := 1;
    }
}

While this syntax can express simple block-based iteration strategies, it is not expressive enough to specify iterations where we skip some elements. We extend the notation of views to add a stride operator:

int[8 bank(2)] a;
v_a = view[w=2, s=2, off=0];

which creates the following view:

When omitted, stride is set to \(1\), which creates a block-like view.

Typing a view

TODO: This section is stale. The new contrains come after shrink and flex being defined.

As mentioned before, views are treated as simple arrays once they are created. An array is defined as follows:

v_a : t[s bank(b)]

where s is the size of the array and b is the banking factor. To typecheck a view, we first need to infer its type, or more specifically, the values for s and b.

First, assume we have the following expression:

t[s_a bank(b_a)] a;
v_a = view[w, s, off] a; // v : t_v[s_v bank (b_v)]

and the assumptions \(s_a \geq b_a\), \(s_v \geq b_v\) and, \(w \leq s_a\).

Inferring the first two components of the view is straigtforward.

\[ t_v = t \\ s_v = w \text{ if } (o + (w - 1) \times s - 1) \leq s_a \]

Next, we need to infer \(b_v\). To do so, we first write down \(b_e\) which the the maximum possible banking factor that \(v_a\) can have given the stride \(s\).

\[ b_e = \frac{b_a}{\text{gcf}(s, b_a)} \]

See this proof to understand how we get this. Using \(b_e\), we can say:

\[ b_v = \min(w, b_e) \]

Note that we don’t use the value of \(o\) in the description of \(b_v\) because of the aforementioned result.

Unrolled loops and views

Since views are just arrays, we can write:

int[8 bank(2)] a;
v_a = view[w=2, off=0] a;
for (j = 0..2) unroll 2 {
    v_a[j] := 1
}

However, we also impose a restriction on the usage of creation of views using and unrolled iterator value. So, the following program is invalid:

for (i = 0..8) unroll 2 {
    v_a = view[w=2, off=i]
}

This is because it is unclear what a view that is generated by a value space (the set of values represented by an index type) is.

Generalization to multiple dimensions

The notation and the semantics can naturally be extended to multidimensional arrays.

int[8 bank(4)][8 bank(4)] a;
v_a = view[w=2, off=0][w=2, off] a;

Limitations

While views significantly improve the expressive power of array iterations, in their current form, they are still more restrictive that iteration patterns defined using a[i + j].

Inexpressible iteration patterns

Skipping with block based views. While it is fairly straightforward to skip elements with simple views, we cannot represent iterations of that both use a view of width more than one and step more than one element. For example, the following iteration pattern cannot be expressed:
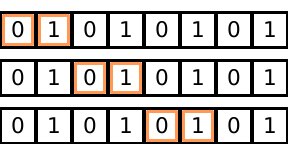
Dynamic strides. Iteration patters where the stride dynamically changes cannot be specified using the view syntax. For example, the following iteration pattern is not expressible.

Inexpressible parallel operations

Currently, Seashell offers no way to express parallelism of the form “read values from two distinct banks in one array, and store their sum in a new memory”

The first inexpressibility can be overcome with a notion of steps in the iterators themselves.

For the second inexpressibility, I don’t see a reason why we can’t also make the stride dynamic now that we are restricting the offset to simple integers.

The final limitation is orthogonal to the concept of views.

Let Rachit know if there are other limitations you can think of.

Constraint operations

Different views need different amounts of hardware depending on their structure. We provide two operators shrink and flex to tell the compiler and the type checker what kind of hardware needs to be added to the in the underlying design.

Note(rachit): Mark mentioned that it might be useful to have a compiler mode where we automatically infer calls to shrink and flex and just warn the user. This definitely makes sense for the use case when someone is trying to get a simple design off the ground and build something.

Shrinking arrays

The shrink operation has the following syntax:

s = shrink(arr, bank_num);

defines a new array s with the underlying array arr and banking factor bank_num. The constraint on bank_num is b % bank_num = 0 where b is the banking factor for arr. While a call to shrink does not create a new memory, it does add new hardware (muxes) to “shrink” the array to the new factor. Specifically, b / bank_num muxes are added to the hardware design and all access to the s go through this additional hardware.

Flexible arrays

The flex operation has the following syntax:

f = flex(arr, )